[!@#$%!]

Originally Posted by schizophrenicroom

i need a math and science credit to get my associates finally, and i already have a stats credit. so i'm taking the credit-by-exam for calculus because that's the only one offered, and i can't take a class because of the money i owe. so i'm stuck taking this calc exam.

i love logic and the arguments/etc and symbols. i was decent at it, and my professor helped. just if this, then that. that made sense to me.

ahhhhh. well if that's your ticket to paradise you have no choice but to learn to love it too. forget about what calculus is not. you can enjoy what is though-- there's real beauty in it. if you complain and listen to complaints your hate will only increase, confirmation bias will set in, your mind will close, and you'll just suffer more. but why suffer?

calculus is a way to count what it can't be counted. it's beautiful! in the case of dfferential calculus, it boils down to dividing 0/0. really. integral calculus is about mutiplying ∞ x 0. that's it really. fun stuff when you realize the problem that it solves-- it measures things that couldn't really be measured otherwise. it's used for all sorts of things from airspace technology to pharmacology, and without it we wouldn't be able to deal with anything with any technology where change happens. calculus is fucking gorgeous.

at the core of it is the problem of limits. how deal with things when they approach zero, or infinite. i'd suggest before you look at calculus, look at limits, and read up on infinitesimals..

there's this stupid joke i like. a mathematician and an engineer want to kiss a girl (that's the version i heard anyway, you can adapt to a less sexist/more updated version). the mathematician approaches halfway. then he approaches halfway again. then half of that. then again half of that distance, etc. he keeps getting closer and closer but never reaches her and concludes he can't kiss her. the engineer on the other hand only need to get as close as needed for all practical purposes. ha ha ha ha.

anyway that mathematician is just another version of zeno's paradox (aka achilles and the turtle), which is one of our earliest ideas about limits-- where things approach when they can't really get there. calculus starts from that.

in differential calculus for example you want to measure the slope of a function.

so in geometry you want to measure the gradient of a straight line you construct a rigt-angled triangle. you take the height and length and divide them and you get the ratio your slope. yes? for x that you move in the horizontal you increase y in the vertical. simple. used all the time in carpentry and construction and all that. the gradient.

 

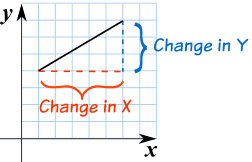
but what when it's not a straight line? what if it's a curve? in each point of this curve the slope is different, yes? how do you measure the slope at each point?

 

to make a long story short-- in order to measure the slope (aka rate of change) at a curve, you take a tiny triangle that gets close to the curve. well that's not close enough to so make the triangle smaller. and smaller. and smaller. until the height and the length of your base approach zero. but you can't divide 0/0 yes? well, calculus sort of figures out how to approach close enough for all practical purposes, ha ha ha ha ha ha ha ha.

anyway, if you think about it-- the derivative (gradient) of a function is also a function. and the relationship between a function and its derivative can be really a thing of beauty.

 

anyway, speaking of functions. how is your algebra? because maybe it's algebra and not calculus that's giving you a hard time. i'd say check your algebra first and then calculus will come easy. won't hurt to review geometry and a little bit of trig first. trig palin.

alright you. best wishes. this can be fun.